Onderzoeksmethoden Research Methods

Categorie: Quantitative Research

  • Podcast Sampling (Chapter 10)

    An Overview of Sampling

    Chapter 10 of the textbook, “Introduction to Statistics in Psychology,” focuses on the key concepts of samples and populations and their role in inferential statistics, which allows researchers to generalize findings from a smaller subset of data to the entire population of interest.

    • Population: The entire set of scores on a particular variable. It’s important to note that in statistics, the term “population” refers specifically to scores, not individuals or entities.
    • Sample: A smaller set of scores selected from the entire population. Samples are used in research due to the practical constraints of studying entire populations, which can be time-consuming and costly.

    Random Samples and Their Characteristics

    The chapter emphasizes the importance of random samples, where each score in the population has an equal chance of being selected. This systematic approach ensures that the sample is representative of the population, reducing bias and increasing the reliability of generalizations.

    Various methods can be used to draw random samples, including using random number generators, tables, or even drawing slips of paper from a hat . The key is to ensure that every score has an equal opportunity to be included.

    The chapter explores the characteristics of random samples, highlighting the tendency of sample means to approximate the population mean, especially with larger sample sizes. Tables 10.2 and 10.3 in the source illustrate this concept, demonstrating how the spread of sample means decreases and clusters closer to the population mean as the sample size increases.

    Standard Error and Confidence Intervals

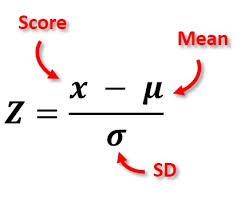
    The chapter introduces standard error, a measure of the variability of sample means drawn from a population. Standard error is essentially the standard deviation of the sample means, reflecting the average deviation of sample means from the population mean.

    • Standard error is inversely proportional to the sample size. Larger samples tend to have smaller standard errors, indicating more precise estimates of the population mean.

    The concept of confidence intervals is also explained. A confidence interval represents a range within which the true population parameter is likely to lie, based on the sample data. The most commonly used confidence level is 95%, meaning that there is a 95% probability that the true population parameter falls within the calculated interval .

    • Confidence intervals provide a way to quantify the uncertainty associated with inferring population characteristics from sample data. A wider confidence interval indicates greater uncertainty, while a narrower interval suggests a more precise estimate.

    Key Points from Chapter 10

    • Understanding the distinction between samples and populations is crucial for applying inferential statistics.
    • Random samples are essential for drawing valid generalizations from research findings.
    • Standard error and confidence intervals provide measures of the variability and uncertainty associated with sample-based estimates of population parameters.

    The chapter concludes by reminding readers that the concepts discussed serve as a foundation for understanding and applying inferential statistics in later chapters, paving the way for more complex statistical tests like t-tests .

  • A/B testing

    In this blog post, we will discuss the basics of A/B testing and provide some examples of how media professionals can use it to improve their content.

    What is A/B Testing?

    A/B testing is a method of comparing two variations of a webpage, email, or advertisement to determine which performs better. The variations are randomly assigned to different groups of users, and their behavior is measured and compared to determine which variation produces better results. The goal of A/B testing is to identify which variations produce better results so that media professionals can make data-driven decisions for future content.

    A/B Testing Examples

    There are many different ways that media professionals can use A/B testing to optimize their content. Below are some examples of how A/B testing can be used in various media contexts.

    1. Email Marketing

    Email marketing is a popular way for media companies to engage with their audience and drive traffic to their website. A/B testing can be used to test different subject lines, email designs, and call-to-action buttons to determine which variations produce the best open and click-through rates.

    For example, a media company could test two different subject lines for an email promoting a new article. One subject line could be straightforward and descriptive, while the other could be more creative and attention-grabbing. By sending these two variations to a sample of their audience, the media company can determine which subject line leads to more opens and clicks, and use that data to improve future email campaigns.

    1. Website Design

    A/B testing can also be used to optimize website design and user experience. By testing different variations of a webpage, media professionals can identify which elements lead to more engagement, clicks, and conversions.

  • Why Use Z-Scores in Statistics

    formula z score

    If you’re a student, researcher, or professional working in the field of statistics, you’ve likely heard of Z-scores. But why use Z-scores in your data analysis? In this blog post, we’ll explain why Z-scores can be so beneficial to your data analysis and provide examples of how to use them in your quantitative research. By the end of this post, you’ll have a better understanding of why Z-scores are so important and how to use them in your research.

    (Image Suggestion: A graph showing a data set represented by Z-scores, highlighting the transformation of the data points in relation to the mean and standard deviation.)

    What are Z-Scores?

    Are you interested in developing a better understanding of statistics and quantitative research? If so, you’ve come to the right place! Today, we will delve into the topic of Z-Scores and their significance in statistics.

    Z-Scores are numerical scores that indicate how many standard deviations an observation is from the mean. In other words, a Z-Score of 0 represents a data point that is exactly equal to the mean. A Z-Score of 1 indicates data one standard deviation above the mean, while -1 represents data one standard deviation below the mean.

    Using Z-Scores enables us to normalize our data and provide context for each value relative to all other values in our dataset. This facilitates the comparison of values from different distributions and helps to minimize bias when evaluating two groups or samples. Furthermore, it provides an overall measure of how distinct a given score is from the mean, which is particularly useful for identifying extreme outliers or determining relative standing within a group or sample.

    Additionally, Z-Scores can also inform us about the probability of a specific value occurring within a dataset, taking its position relative to the mean into account. This additional feature enhances the usefulness of Z-Scores when interpreting quantitative research results. Each distribution has its own set of unique probabilities associated with specific scores, and understanding this information empowers us to make more informed decisions regarding our datasets and draw meaningful conclusions from them.

    Understanding the Benefits of Using Z-Scores in Statistics

    Are you searching for a method to compare two datasets or interpret statistical results? If so, using Z-scores could be the solution. Z-scores are a statistical tool employed to determine the distance of an individual measurement from the mean value in a given dataset. This facilitates data comparison across different sample sizes and distributions, as well as the identification of outliers and trends.

    The use of Z-scores offers numerous advantages over alternative statistics like raw scores or percentages. For instance, as it is not affected by outliers or extremes, it can yield more accurate outcomes compared to raw scores. Moreover, it is non-directional, disregarding whether a score is above or below the mean, making result interpretation less complicated.

    Utilizing Z-scores also permits the quantification of individual performance in relation to a larger group, offering valuable insights into data set variability. Additionally, it provides a simple way to identify subtle patterns and trends that might be overlooked using other quantitative analysis methods like linear regression or chi-square tests. Finally, when employed in hypothesis testing, Z-scores aid in calculating confidence intervals. This allows for more precise measurements of the level of confidence one can have in their conclusions based on the sample size and distribution type.

    Overall, correct comprehension and application of Z-scores can deliver significant benefits in statistical research and analysis, empowering more accurate decision-making.

    Examples of How to Use Z-Scores in Quantitative Research

    In quantitative research, z-scores are a useful tool for analyzing data and making informed decisions. Z-scores allow you to compare variables from different distributions, quantify how much a value differs from the mean, and make statements about the significance of results for inference testing. They are also used to standardize data, which can be used for comparison purposes and detect outliers in data sets.

    Z-scores can be especially helpful when looking at two or more sets of data by converting them to a common scale. Using z-scores allows you to compare and analyze data from different populations without having to adjust for differences in magnitude between the two datasets. Z-scores can also help you identify relationships between variables in your quantitative research study, as well as determine statistical significance between two or more sets of data.

    In addition, z-scores can be used to standardize data within a population, which is important for making proper inferences about the data. Finally, z-scores can be used to calculate correlation coefficients that measure the degree of linear association between two variables. All these uses make z-scores an invaluable tool in quantitative research that should not be overlooked!

    In Conclusion

    Z-scores are powerful tools for data analysis and quantitative research, making them invaluable assets in any statistician’s arsenal. Their ability to standardize data across distributions, identify outliers, and measure correlation coefficients makes them must-haves for all statistical research. With a better understanding of Z-scores, you can make more informed decisions based on your data sets and draw meaningful conclusions from your quantitative research. So don’t wait – start utilizing the power of Z-scores to improve your results today!