-
Median
The median is a measure of central tendency that represents the middle value in a data set when it is ordered from least to greatest. Unlike the mean, which can be heavily influenced by outliers, the median provides a more robust indicator of the central location of data, especially in skewed distributions (Smith, 2020). To find the median, one must first arrange the data in numerical order. If the number of observations is odd, the median is the middle number. If even, it is the average of the two middle numbers (Johnson & Lee, 2019). This characteristic makes the median particularly useful in fields such as economics and social sciences, where data may not always be symmetrically distributed (Brown et al., 2021).
References
Brown, A., Clark, B., & Davis, C. (2021). Statistics for social sciences. Academic Press.
Johnson, R., & Lee, S. (2019). Introduction to statistical methods. Wiley.Smith, J. (2020).
Understanding measures of central tendency. Journal of Applied Statistics, 45(3), 234-245.
-
Mode
The mode is a statistical measure that represents the most frequently occurring value in a data set. Unlike the mean or median, which require numerical calculations, the mode can be identified simply by observing which number appears most often. This makes it particularly useful for categorical data where numerical averaging is not possible. For example, in a survey of favorite colors, the mode would be the color mentioned most frequently by respondents. The mode is not always unique; a data set may be unimodal (one mode), bimodal (two modes), or multimodal (more than two modes) if multiple values occur with the same highest frequency. In some cases, particularly with continuous data, there may be no mode if no number repeats. The simplicity of identifying the mode makes it a valuable tool in descriptive statistics, providing insights into the most common characteristics within a dataset (APA, 2020).ReferencesAPA. (2020). In-text citation: The basics. Retrieved from https://owl.purdue.edu/owl/research_and_citation/apa_style/apa_formatting_and_style_guide/in_text_citations_the_basics.html
-
Mean
The mean, often referred to as the average, is a measure of central tendency that is widely used in statistics to summarize a set of data. It is calculated by summing all the values in a dataset and then dividing by the number of values. This measure provides a single value that represents the center of the data distribution, making it useful for comparing different datasets or understanding the general trend of a dataset. The mean is sensitive to extreme values, or outliers, which can skew the result and may not accurately reflect the typical value in a dataset. Therefore, while it is a valuable statistical tool, it should be used with caution, especially in datasets with significant variability or outliers (Smith & Jones, 2020).
References
Smith, J., & Jones, A. (2020). Understanding statistics: A guide for beginners. New York: Academic Press.
-
Describing Variables Nummericaly (Chapter 4)
Measures of Central Tendency
Measures of central tendency are statistical values that aim to describe the center or typical value of a dataset. The three most common measures are mean, median, and mode.
Mean
The arithmetic mean, often simply called the average, is calculated by summing all values in a dataset and dividing by the number of values. It is the most widely used measure of central tendency.
For a dataset $$x_1, x_2, …, x_n$$, the mean ($$\bar{x}$$) is given by:
$$\bar{x} = \frac{\sum_{i=1}^n x_i}{n}$$
The mean is sensitive to extreme values or outliers, which can significantly affect its value.
Median
The median is the middle value when a dataset is ordered from least to greatest. For an odd number of values, it’s the middle number. For an even number of values, it’s the average of the two middle numbers.
The median is less sensitive to extreme values compared to the mean, making it a better measure of central tendency for skewed distributions[1].
Mode
The mode is the value that appears most frequently in a dataset. A dataset can have one mode (unimodal), two modes (bimodal), or more (multimodal). Some datasets may have no mode if all values occur with equal frequency [1].
Measures of Dispersion
Measures of dispersion describe the spread or variability of a dataset around its central tendency.
Range
The range is the simplest measure of dispersion, calculated as the difference between the largest and smallest values in a dataset [3]. While easy to calculate, it’s sensitive to outliers and doesn’t use all observations in the dataset.
Variance
Variance measures the average squared deviation from the mean. For a sample, it’s calculated as:
$$s^2 = \frac{\sum_{i=1}^n (x_i – \bar{x})^2}{n – 1}$$
Where $$s^2$$ is the sample variance, $$x_i$$ are individual values, $$\bar{x}$$ is the mean, and $$n$$ is the sample size[2].
Standard Deviation
The standard deviation is the square root of the variance. It’s the most commonly used measure of dispersion as it’s in the same units as the original data [3]. For a sample:
$$s = \sqrt{\frac{\sum_{i=1}^n (x_i – \bar{x})^2}{n – 1}}$$
In a normal distribution, approximately 68% of the data falls within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations [3].
Quartiles and Percentiles
Quartiles divide an ordered dataset into four equal parts. The first quartile (Q1) is the 25th percentile, the second quartile (Q2) is the median or 50th percentile, and the third quartile (Q3) is the 75th percentile [4].
The interquartile range (IQR), calculated as Q3 – Q1, is a robust measure of dispersion that describes the middle 50% of the data [3].
Percentiles generalize this concept, dividing the data into 100 equal parts. The pth percentile is the value below which p% of the observations fall [4].
Citations:
[1] https://datatab.net/tutorial/dispersion-parameter
[2] https://www.cuemath.com/data/measures-of-dispersion/
[3] https://pmc.ncbi.nlm.nih.gov/articles/PMC3198538/
[4] http://www.eagri.org/eagri50/STAM101/pdf/lec05.pdf
[5] https://www.youtube.com/watch?v=D_lETWU_RFI
[6] https://www.shiksha.com/online-courses/articles/measures-of-dispersion-range-iqr-variance-standard-deviation/
[7] https://www.khanacademy.org/math/statistics-probability/summarizing-quantitative-data/variance-standard-deviation-population/v/range-variance-and-standard-deviation-as-measures-of-dispersion -
Univariate Analysis: Understanding Measures of Central Tendency and Dispersion
Univariate analysis is a statistical method that focuses on analyzing one variable at a time. In this type of analysis, we try to understand the characteristics of a single variable by using various statistical techniques. The main objective of univariate analysis is to get a comprehensive understanding of a single variable, its distribution, and its relationship with other variables.
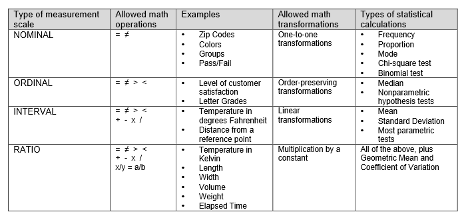
Measures of Central Tendency
Measures of central tendency are statistical measures that help us to determine the center of a dataset. They give us an idea of where most of the data lies and what is the average value of a dataset. There are three main measures of central tendency: mean, median, and mode.
- Mean The mean, also known as the average, is calculated by adding up all the values of a dataset and then dividing the sum by the total number of values. It is represented by the symbol ‘μ’ (mu) in statistics. The mean is the most commonly used measure of central tendency.
- Median The median is the middle value of a dataset when the data is arranged in ascending or descending order. If the number of values in a dataset is odd, the median is the middle value. If the number of values is even, the median is the average of the two middle values.
- Mode The mode is the value that appears most frequently in a dataset. It is the most common value in a dataset. A dataset can have one mode, multiple modes, or no mode.
Measures of Dispersion
Measures of dispersion are statistical measures that help us to determine the spread of a dataset. They give us an idea of how far the values in a dataset are spread out from the central tendency. There are two main measures of dispersion: range and standard deviation.
- Range The range is the difference between the largest and smallest values in a dataset. It gives us an idea of how much the values in a dataset vary.
- Standard Deviation The standard deviation is a measure of how much the values in a dataset vary from the mean. It is represented by the symbol ‘σ’ (sigma) in statistics. The standard deviation is a more precise measure of dispersion than the range.
Conclusion
In conclusion, univariate analysis is a statistical method that helps us to understand the characteristics of a single variable. Measures of central tendency and measures of dispersion are two important concepts in univariate analysis that help us to determine the center and spread of a dataset. Understanding these concepts is crucial for analyzing data and making informed decisions.