Onderzoeksmethoden Research Methods

Tag: Quantitative

  • Dependent t-test

    The dependent t-test, also known as the paired samples t-test, is a statistical method used to compare the means of two related groups, allowing researchers to assess whether significant differences exist under different conditions or over time. This test is particularly relevant in educational and psychological research, where it is often employed to analyze the impact of interventions on the same subjects. By measuring participants at two different points—such as before and after a treatment or training program—researchers can identify changes in outcomes, thus making it a valuable tool for evaluating the effectiveness of educational strategies and interventions in various contexts, including first-year university courses.

    Notably, the dependent t-test is underpinned by several key assumptions, including the requirement that the data be continuous, the observations be paired, and the differences between pairs be approximately normally distributed. Understanding these assumptions is critical, as violations can lead to inaccurate conclusions and undermine the test’s validity.

    Common applications of the dependent t-test include pre-test/post-test studies and matched sample designs, where participants are assessed on a particular variable before and after an intervention.

    Overall, the dependent t-test remains a fundamental statistical tool in academic research, with its ability to reveal insights into the effectiveness of interventions and programs. As such, mastering its application and interpretation is essential for first-year university students engaged in quantitative research methodologies.

    Assumptions When conducting a dependent t-test, it is crucial to ensure that certain assumptions are met to validate the results. Understanding these assumptions can help you identify potential issues in your data and provide alternatives if necessary.

    Assumption 1: Continuous Dependent Variable The first assumption states that the dependent variable must be measured on a continuous scale, meaning it should be at the interval or ratio level. Examples of appropriate variables include revision time (in hours), intelligence (measured using IQ scores), exam performance (scaled from 0 to 100), and weight (in kilograms).

    Assumption 2: Paired Observations The second assumption is that the data should consist of paired observations, which means each participant is measured under two different conditions. This ensures that the data is related, allowing for the analysis of differences within the same subjects.

    Assumption 3: No Significant Outliers The third assumption requires that there be no significant outliers in the differences between the paired groups. Outliers are data points that differ markedly from others and can adversely affect the results of the dependent t-test, potentially leading to invalid conclusions.

    Assumption 4: Normality of Differences The fourth assumption states that the distribution of the differences in the dependent variable should be approximately normally distributed, especially important for smaller sample sizes (N < 25)[5]. While real-world data often deviates from perfect normality, the results of a dependent t-test can still be valid if the distribution is roughly symmetric and bell-shaped.

    Common applications of the dependent t-test include pre-test/post-test studies and matched pairs designs. Scenarios for Application Repeated Measures One of the primary contexts for using the dependent t-test is in repeated measures designs. In such studies, the same subjects are measured at two different points in time or under two different conditions. For example, researchers might measure the physical performance of athletes before and after a training program, analyzing whether significant improvements occurred as a result of the intervention.

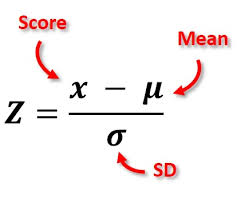
    Hypothesis Testing In conducting a dependent t-test, researchers typically formulate two hypotheses: the null hypothesis (H0) posits that there is no difference in the means of the paired groups, while the alternative hypothesis (H1) suggests that a significant difference exists. By comparing the means and calculating the test statistic, researchers can determine whether to reject or fail to reject the null hypothesis, providing insights into the effectiveness of an intervention or treatment.

    , , , ,

  • Independent t-test

    The independent t-test, also known as the two-sample t-test or unpaired t-test, is a fundamental statistical method used to assess whether the means of two unrelated groups are significantly different from one another. This inferential test is particularly valuable in various fields, including psychology, medicine, and social sciences, as it allows researchers to draw conclusions about population parameters based on sample data when the assumptions of normality and equal variances are met. Its development can be traced back to the early 20th century, primarily attributed to William Sealy Gosset, who introduced the concept of the t-distribution to handle small sample sizes, thereby addressing limitations in traditional hypothesis testing methods. The independent t-test plays a critical role in data analysis by providing a robust framework for hypothesis testing, facilitating data-driven decision-making across disciplines. Its applicability extends to real-world scenarios, such as comparing the effectiveness of different treatments or assessing educational outcomes among diverse student groups.

    The test’s significance is underscored by its widespread usage and enduring relevance in both academic and practical applications, making it a staple tool for statisticians and researchers alike. However, the independent t-test is not without its controversies and limitations. Critics point to its reliance on key assumptions—namely, the independence of samples, normality of the underlying populations, and homogeneity of variances—as potential pitfalls that can compromise the validity of results if violated.

    Moreover, the test’s sensitivity to outliers and the implications of sample size on generalizability further complicate its application, necessitating careful consideration and potential alternative methods when these assumptions are unmet. Despite these challenges, the independent t-test remains a cornerstone of statistical analysis, instrumental in hypothesis testing and facilitating insights across various research fields. As statistical practices evolve, ongoing discussions around its assumptions and potential alternatives continue to shape its application, reflecting the dynamic nature of data analysis methodologies in contemporary research.

    , , , , , ,

  • Podcast Statistical Significance (Chapter 11)

    Statistical significance is a fundamental concept that first-year university students must grasp to effectively interpret and conduct research across various disciplines. Understanding this concept is crucial for developing critical thinking skills and evaluating the validity of scientific claims.

    At its core, statistical significance refers to the likelihood that an observed effect or relationship in a study occurred by chance rather than due to a true underlying phenomenon[2]. This likelihood is typically expressed as a p-value, which represents the probability of obtaining results at least as extreme as those observed, assuming the null hypothesis is true[2].

    The significance level, often denoted as alpha (α), is a threshold set by researchers to determine whether a result is considered statistically significant. Commonly, this level is set at 0.05 or 5%[2]. If the p-value falls below this threshold, the result is deemed statistically significant, indicating strong evidence against the null hypothesis[2].

    For first-year students, it’s essential to understand that statistical significance does not necessarily imply practical importance or real-world relevance. A result can be statistically significant due to a large sample size, even if the effect size is small[2]. Conversely, a practically important effect might not reach statistical significance in a small sample.

    When interpreting research findings, students should consider both statistical significance and effect size. Effect size measures the magnitude of the observed relationship or difference, providing context for the practical importance of the results[2].

    It’s also crucial for students to recognize that statistical significance is not infallible. The emphasis on p-values has contributed to publication bias and a replication crisis in some fields, where statistically significant results are more likely to be published, potentially leading to an overestimation of effects[2].

    To develop statistical literacy, first-year students should practice calculating and interpreting descriptive statistics and creating data visualizations[1]. These skills form the foundation for understanding more complex statistical concepts and procedures[1].

    As students progress in their academic careers, they will encounter various statistical tests and methods. However, the fundamental concept of statistical significance remains central to interpreting research findings across disciplines.

    In conclusion, grasping the concept of statistical significance is vital for first-year university students as they begin to engage with academic research. It provides a framework for evaluating evidence and making informed decisions based on data. However, students should also be aware of its limitations and the importance of considering other factors, such as effect size and practical significance, when interpreting research findings. By developing a strong foundation in statistical literacy, students will be better equipped to critically analyze and contribute to research in their chosen fields.

    Citations:
    [1] https://files.eric.ed.gov/fulltext/EJ1339553.pdf
    [2] https://www.scribbr.com/statistics/statistical-significance/
    [3] https://pmc.ncbi.nlm.nih.gov/articles/PMC8107779/
    [4] https://www.sciencedirect.com/science/article/pii/S0346251X22000409
    [5] https://www.researchgate.net/publication/354377037_EXPLORING_FIRST_YEAR_UNIVERSITY_STUDENTS’_STATISTICAL_LITERACY_A_CASE_ON_DESCRIBING_AND_VISUALIZING_DATA
    [6] https://www.researchgate.net/publication/264315744_Assessment_experience_of_first-year_university_students_dealing_with_the_unfamiliar
    [7] https://core.ac.uk/download/pdf/40012726.pdf
    [8] https://www.cram.com/essay/The-Importance-Of-Statistics-At-University-Students/F326ACMLG6445

  • Longitudinal Quantitative Research

    Observing Change Over Time

    Longitudinal research is a powerful research design that involves repeatedly collecting data from the same individuals or groups over a period of time, allowing researchers to observe how phenomena change and develop. Unlike cross-sectional studies, which capture a snapshot of a population at a single point in time, longitudinal research captures the dynamic nature of social life, providing a deeper understanding of cause-and-effect relationships, trends, and patterns.

    Longitudinal studies can take on various forms, depending on the research question, timeframe, and resources available. Two common types are:

    Prospective longitudinal studies: Researchers establish the study from the beginning and follow the participants forward in time. This approach allows researchers to plan data collection points and track changes as they unfold.

    Retrospective longitudinal studies: Researchers utilize existing data from the past, such as medical records or historical documents, to construct a timeline and analyze trends over time. This approach can be valuable when studying events that have already occurred or when prospective data collection is not feasible.

    Longitudinal research offers several advantages, including:

    • Tracking individual changes: By following the same individuals over time, researchers can observe how their attitudes, behaviors, or circumstances evolve, providing insights into individual growth and development.2
    • Identifying causal relationships: Longitudinal data can help establish the temporal order of events, strengthening the evidence for causal relationships.1 For example, a study that tracks individuals’ smoking habits and health outcomes over time can provide stronger evidence for the link between smoking and disease than a cross-sectional study.
    • Studying rare events or long-term processes: Longitudinal research is well-suited for investigating events that occur infrequently or phenomena that unfold over extended periods, such as the development of chronic diseases or the impact of social policies on communities.

      However, longitudinal research also presents challenges:
    • Cost and time commitment: Longitudinal studies require significant resources and time investments, particularly for large-scale projects that span many years.
    • Data management: Collecting, storing, and analyzing data over time can be complex and require specialized expertise.
    • Attrition: Participants may drop out of the study over time due to various reasons, such as relocation, loss of interest, or death. Attrition can bias the results if those who drop out differ systematically from those who remain in the study.

    Researchers utilize a variety of data collection methods in longitudinal studies, including surveys, interviews, observations, and document analysis. The choice of methods depends on the research question and the nature of the data being collected.

    A key aspect of longitudinal research design is the selection of an appropriate sample. Researchers may use probability sampling techniques, such as stratified sampling, to ensure a representative sample of the population of interest. Alternatively, they may employ purposive sampling techniques to select individuals with specific characteristics or experiences relevant to the research question.

    • Millennium Cohort Study: This large-scale prospective study tracks the development of children born in the UK in the year 2000, collecting data on their health, education, and well-being at regular intervals.
    • Study on children’s experiences with smoking: This study employed both longitudinal and cross-sectional designs to examine how children’s exposure to smoking and their own smoking habits change over time.
    • Study on the experiences of individuals participating in an employment program: This qualitative study used longitudinal interviews to track participants’ progress and understand their experiences with the program over time.

    Longitudinal research plays a crucial role in advancing our understanding of human behavior and social processes. By capturing change over time, these studies can provide valuable insights into complex phenomena and inform policy decisions, interventions, and theoretical development.

    EXAMPLE SETUP

    Research Question: Does exposure to social media impact the mental health of media students over time? 

    Hypothesis: Media students who spend more time on social media will experience a decline in mental health over time compared to those who spend less time on social media. 

    Methodology: 

    Participants: The study will recruit 100 media students, aged 18-25, who are currently enrolled in a media program at a university. 

    Data Collection: The study will collect data through online surveys administered at three time points: at the beginning of the study (Time 1), six months later (Time 2), and 12 months later (Time 3). The survey will consist of a series of questions about social media use (e.g., hours per day, types of social media used), as well as standardized measures of mental health (e.g., the Patient Health Questionnaire-9 for depression and the Generalized Anxiety Disorder-7 for anxiety). 

    Data Analysis: The study will use linear mixed-effects models to analyze the data, examining the effect of social media use on mental health outcomes over time while controlling for potential confounding variables (e.g., age, gender, prior mental health history). 

    Example Findings: After analyzing the data, the study finds that media students who spend more time on social media experience a significant decline in mental health over time compared to those who spend less time on social media. Specifically, students who spent more than 2 hours per day on social media at Time 1 experienced a 10% increase in depression symptoms and a 12% increase in anxiety symptoms at Time 3 compared to those who spent less than 1 hour per day on social media. These findings suggest that media students should be mindful of their social media use to protect their mental health 

  • Cohort Study

    A cohort study is a specific type of longitudinal research design that focuses on a group of individuals who share a common characteristic, often their age or birth year, referred to as a cohort. Researchers track these individuals over time, collecting data at predetermined intervals to observe how their experiences, behaviors, and outcomes evolve. This approach enables researchers to investigate how various factors influence the cohort’s development and identify potential trends or patterns within the group12.

    Cohort studies stand out for their ability to reveal changes within individuals’ lives, offering insights into cause-and-effect relationships that other research designs may miss. For example, a cohort study might track a group of students throughout their university experience to examine how alcohol consumption patterns change over time and relate those changes to academic performance, social interactions, or health outcomes3.

    Researchers can design cohort studies on various scales and timeframes. Large-scale studies, such as the Millennium Cohort Study, often involve thousands of participants and continue for many years, requiring significant resources and a team of researchers2. Smaller cohort studies can focus on more specific events or shorter time periods. For instance, researchers could interview a group of people before, during, and after a significant life event, like a job loss or a natural disaster, to understand its impact on their well-being and coping mechanisms2.

    There are two primary types of cohort studies:

    Prospective cohort studies are established from the outset with the intention of tracking the cohort forward in time.

    Retrospective cohort studies rely on existing data from the past, such as medical records or survey responses, to reconstruct the cohort’s history and analyze trends.

    While cohort studies commonly employ quantitative data collection methods like surveys and statistical analysis, researchers can also incorporate qualitative methods, such as in-depth interviews, to gain a richer understanding of the cohort’s experiences. For example, in a study examining the effectiveness of a new employment program for individuals receiving disability benefits, researchers conducted initial in-depth interviews with participants and followed up with telephone interviews after three and six months to track their progress and gather detailed feedback4.

    To ensure a representative and meaningful sample, researchers employ various sampling techniques in cohort studies. In large-scale studies, stratified sampling is often used to ensure adequate representation of different subgroups within the population25. For smaller studies or when specific characteristics are of interest, purposive sampling can be used to select individuals who meet certain criteria6.

    Researchers must carefully consider the ethical implications of cohort studies, especially when working with vulnerable populations or sensitive topics. Ensuring informed consent, maintaining confidentiality, and minimizing potential harm to participants are paramount throughout the study7.

    Cohort studies are a powerful tool for examining change over time and gaining insights into complex social phenomena. By meticulously tracking a cohort of individuals, researchers can uncover trends, identify potential causal relationships, and contribute valuable knowledge to various fields of study. However, researchers must carefully consider the challenges and ethical considerations associated with these studies to ensure their rigor and validity.

    1. Research question: Start by defining a clear research question for each cohort, such as “What is the effect of social media use on the academic performance of first-year media students compared to third-year media students over a two-year period?” 
    1. Sampling: Decide on the population of interest for each cohort, such as first-year media students and third-year media students at a particular university, and then select a representative sample for each cohort. This can be done through a random sampling method or by selecting participants who meet specific criteria (e.g., enrolled in a particular media program and in their first or third year). 
    1. Data collection: Collect data from the participants in each cohort at the beginning of the study, and then at regular intervals over the two-year period (e.g., every six months). The data can be collected through surveys, interviews, or observation. 
    1. Variables: Identify the dependent and independent variables for each cohort. In this case, the independent variable would be social media use and the dependent variable would be academic performance (measured by GPA, test scores, or other academic indicators). For the second cohort, the time in the media program might also be a variable of interest. 
    1. Analysis: Analyze the data for each cohort separately using appropriate statistical methods to determine if there is a significant relationship between social media use and academic performance. This can include correlation analysis, regression analysis, or other statistical techniques. 
    1. Results and conclusions: Draw conclusions based on the analysis for each cohort and compare the results between the two cohorts. Determine if the results support or refute the research hypotheses for each cohort and make recommendations for future research or practical applications based on the findings.
    2. Ethical considerations: Ensure that the study is conducted ethically for each cohort, with appropriate informed consent and confidentiality measures in place. Obtain necessary approvals from ethics committees or institutional review boards as required for each cohort  

  • Bi-Modal Distribution

    A bi-modal distribution is a statistical distribution that has two peaks in its frequency distribution curve, indicating that there are two distinct groups or subpopulations within the data set. These peaks can be roughly equal in size, or one peak may be larger than the other. In either case, the bi-modal distribution is a useful tool for identifying and analyzing patterns in data. 

    One example of a bi-modal distribution can be found in the distribution of heights among adult humans. The first peak in the distribution corresponds to the average height of adult women, which is around 5 feet 4 inches (162.6 cm). The second peak corresponds to the average height of adult men, which is around 5 feet 10 inches (177.8 cm). The two peaks in this distribution are clearly distinct, indicating that there are two distinct groups of people with different average heights. 

    To illustrate this bi-modal distribution, we can plot a frequency distribution histogram of heights of adult humans. The histogram would have two distinct peaks, one corresponding to the heights of women and the other corresponding to the heights of men. The histogram would also show that there is very little overlap between these two groups, indicating that they are largely distinct. 

    One of the main reasons why bi-modal distributions are important is that they can provide insights into the underlying structure of a data set. For example, in the case of the distribution of heights among adult humans, the bi-modal distribution indicates that there are two distinct groups with different average heights. This could be useful for a range of applications, from designing clothing to developing medical treatments. 

    Another example of a bi-modal distribution can be found in the distribution of income among households in the United States. The first peak in this distribution corresponds to households with low to moderate income, while the second peak corresponds to households with high income. This bi-modal distribution has been studied extensively by economists and policy makers, as it has important implications for issues such as income inequality and economic growth. 

    In conclusion, bi-modal distributions are a useful tool for identifying and analyzing patterns in data. They can provide insights into the underlying structure of a data set, and can be useful for a range of applications. The distribution of heights among adult humans and the distribution of income among households in the United States are two examples of bi-modal distributions that have important implications for a range of fields. A better understanding of bi-modal distributions can help us make better decisions and develop more effective solutions to complex problems. 

  • Podcast Sampling (Chapter 10)

    An Overview of Sampling

    Chapter 10 of the textbook, “Introduction to Statistics in Psychology,” focuses on the key concepts of samples and populations and their role in inferential statistics, which allows researchers to generalize findings from a smaller subset of data to the entire population of interest.

    • Population: The entire set of scores on a particular variable. It’s important to note that in statistics, the term “population” refers specifically to scores, not individuals or entities.
    • Sample: A smaller set of scores selected from the entire population. Samples are used in research due to the practical constraints of studying entire populations, which can be time-consuming and costly.

    Random Samples and Their Characteristics

    The chapter emphasizes the importance of random samples, where each score in the population has an equal chance of being selected. This systematic approach ensures that the sample is representative of the population, reducing bias and increasing the reliability of generalizations.

    Various methods can be used to draw random samples, including using random number generators, tables, or even drawing slips of paper from a hat . The key is to ensure that every score has an equal opportunity to be included.

    The chapter explores the characteristics of random samples, highlighting the tendency of sample means to approximate the population mean, especially with larger sample sizes. Tables 10.2 and 10.3 in the source illustrate this concept, demonstrating how the spread of sample means decreases and clusters closer to the population mean as the sample size increases.

    Standard Error and Confidence Intervals

    The chapter introduces standard error, a measure of the variability of sample means drawn from a population. Standard error is essentially the standard deviation of the sample means, reflecting the average deviation of sample means from the population mean.

    • Standard error is inversely proportional to the sample size. Larger samples tend to have smaller standard errors, indicating more precise estimates of the population mean.

    The concept of confidence intervals is also explained. A confidence interval represents a range within which the true population parameter is likely to lie, based on the sample data. The most commonly used confidence level is 95%, meaning that there is a 95% probability that the true population parameter falls within the calculated interval .

    • Confidence intervals provide a way to quantify the uncertainty associated with inferring population characteristics from sample data. A wider confidence interval indicates greater uncertainty, while a narrower interval suggests a more precise estimate.

    Key Points from Chapter 10

    • Understanding the distinction between samples and populations is crucial for applying inferential statistics.
    • Random samples are essential for drawing valid generalizations from research findings.
    • Standard error and confidence intervals provide measures of the variability and uncertainty associated with sample-based estimates of population parameters.

    The chapter concludes by reminding readers that the concepts discussed serve as a foundation for understanding and applying inferential statistics in later chapters, paving the way for more complex statistical tests like t-tests .

  • A/B testing

    In this blog post, we will discuss the basics of A/B testing and provide some examples of how media professionals can use it to improve their content.

    What is A/B Testing?

    A/B testing is a method of comparing two variations of a webpage, email, or advertisement to determine which performs better. The variations are randomly assigned to different groups of users, and their behavior is measured and compared to determine which variation produces better results. The goal of A/B testing is to identify which variations produce better results so that media professionals can make data-driven decisions for future content.

    A/B Testing Examples

    There are many different ways that media professionals can use A/B testing to optimize their content. Below are some examples of how A/B testing can be used in various media contexts.

    1. Email Marketing

    Email marketing is a popular way for media companies to engage with their audience and drive traffic to their website. A/B testing can be used to test different subject lines, email designs, and call-to-action buttons to determine which variations produce the best open and click-through rates.

    For example, a media company could test two different subject lines for an email promoting a new article. One subject line could be straightforward and descriptive, while the other could be more creative and attention-grabbing. By sending these two variations to a sample of their audience, the media company can determine which subject line leads to more opens and clicks, and use that data to improve future email campaigns.

    1. Website Design

    A/B testing can also be used to optimize website design and user experience. By testing different variations of a webpage, media professionals can identify which elements lead to more engagement, clicks, and conversions.

  • Why Use Z-Scores in Statistics

    formula z score

    If you’re a student, researcher, or professional working in the field of statistics, you’ve likely heard of Z-scores. But why use Z-scores in your data analysis? In this blog post, we’ll explain why Z-scores can be so beneficial to your data analysis and provide examples of how to use them in your quantitative research. By the end of this post, you’ll have a better understanding of why Z-scores are so important and how to use them in your research.

    (Image Suggestion: A graph showing a data set represented by Z-scores, highlighting the transformation of the data points in relation to the mean and standard deviation.)

    What are Z-Scores?

    Are you interested in developing a better understanding of statistics and quantitative research? If so, you’ve come to the right place! Today, we will delve into the topic of Z-Scores and their significance in statistics.

    Z-Scores are numerical scores that indicate how many standard deviations an observation is from the mean. In other words, a Z-Score of 0 represents a data point that is exactly equal to the mean. A Z-Score of 1 indicates data one standard deviation above the mean, while -1 represents data one standard deviation below the mean.

    Using Z-Scores enables us to normalize our data and provide context for each value relative to all other values in our dataset. This facilitates the comparison of values from different distributions and helps to minimize bias when evaluating two groups or samples. Furthermore, it provides an overall measure of how distinct a given score is from the mean, which is particularly useful for identifying extreme outliers or determining relative standing within a group or sample.

    Additionally, Z-Scores can also inform us about the probability of a specific value occurring within a dataset, taking its position relative to the mean into account. This additional feature enhances the usefulness of Z-Scores when interpreting quantitative research results. Each distribution has its own set of unique probabilities associated with specific scores, and understanding this information empowers us to make more informed decisions regarding our datasets and draw meaningful conclusions from them.

    Understanding the Benefits of Using Z-Scores in Statistics

    Are you searching for a method to compare two datasets or interpret statistical results? If so, using Z-scores could be the solution. Z-scores are a statistical tool employed to determine the distance of an individual measurement from the mean value in a given dataset. This facilitates data comparison across different sample sizes and distributions, as well as the identification of outliers and trends.

    The use of Z-scores offers numerous advantages over alternative statistics like raw scores or percentages. For instance, as it is not affected by outliers or extremes, it can yield more accurate outcomes compared to raw scores. Moreover, it is non-directional, disregarding whether a score is above or below the mean, making result interpretation less complicated.

    Utilizing Z-scores also permits the quantification of individual performance in relation to a larger group, offering valuable insights into data set variability. Additionally, it provides a simple way to identify subtle patterns and trends that might be overlooked using other quantitative analysis methods like linear regression or chi-square tests. Finally, when employed in hypothesis testing, Z-scores aid in calculating confidence intervals. This allows for more precise measurements of the level of confidence one can have in their conclusions based on the sample size and distribution type.

    Overall, correct comprehension and application of Z-scores can deliver significant benefits in statistical research and analysis, empowering more accurate decision-making.

    Examples of How to Use Z-Scores in Quantitative Research

    In quantitative research, z-scores are a useful tool for analyzing data and making informed decisions. Z-scores allow you to compare variables from different distributions, quantify how much a value differs from the mean, and make statements about the significance of results for inference testing. They are also used to standardize data, which can be used for comparison purposes and detect outliers in data sets.

    Z-scores can be especially helpful when looking at two or more sets of data by converting them to a common scale. Using z-scores allows you to compare and analyze data from different populations without having to adjust for differences in magnitude between the two datasets. Z-scores can also help you identify relationships between variables in your quantitative research study, as well as determine statistical significance between two or more sets of data.

    In addition, z-scores can be used to standardize data within a population, which is important for making proper inferences about the data. Finally, z-scores can be used to calculate correlation coefficients that measure the degree of linear association between two variables. All these uses make z-scores an invaluable tool in quantitative research that should not be overlooked!

    In Conclusion

    Z-scores are powerful tools for data analysis and quantitative research, making them invaluable assets in any statistician’s arsenal. Their ability to standardize data across distributions, identify outliers, and measure correlation coefficients makes them must-haves for all statistical research. With a better understanding of Z-scores, you can make more informed decisions based on your data sets and draw meaningful conclusions from your quantitative research. So don’t wait – start utilizing the power of Z-scores to improve your results today!