-
Correlation Spearman and Pearson
Correlation is a fundamental concept in statistics that measures the strength and direction of the relationship between two variables. For first-year media students, understanding correlation is crucial for analyzing data trends and making informed decisions. This essay will explore two common correlation coefficients: Pearson’s r and Spearman’s rho.
Pearson’s Correlation Coefficient (r)
Pearson’s r is used to measure the linear relationship between two continuous variables. It ranges from -1 to +1, where:
- +1 indicates a perfect positive linear relationship
- 0 indicates no linear relationship
- -1 indicates a perfect negative linear relationship
The formula for Pearson’s r is:
$$r = \frac{\sum_{i=1}^{n} (x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i – \bar{x})^2 \sum_{i=1}^{n} (y_i – \bar{y})^2}}$$
Where:
- $$x_i$$ and $$y_i$$ are individual values
- $$\bar{x}$$ and $$\bar{y}$$ are the means of x and y
Example: A media researcher wants to investigate the relationship between the number of social media posts and engagement rates. They collect data from 50 social media campaigns and calculate Pearson’s r to be 0.75. This indicates a strong positive linear relationship between the number of posts and engagement rates.
Spearman’s Rank Correlation Coefficient (ρ)
Spearman’s rho is used when data is ordinal or does not meet the assumptions for Pearson’s r. It measures the strength and direction of the monotonic relationship between two variables.
The formula for Spearman’s rho is:
$$\rho = 1 – \frac{6 \sum d_i^2}{n(n^2 – 1)}$$
Where:
- $$d_i$$ is the difference between the ranks of corresponding values
- n is the number of pairs of values
Example: A researcher wants to study the relationship between a TV show’s IMDB rating and its viewership ranking. They use Spearman’s rho because the data is ordinal. A calculated ρ of 0.85 would indicate a strong positive monotonic relationship between IMDB ratings and viewership rankings.
Significance and Significance Level
When interpreting correlation coefficients, it’s crucial to consider their statistical significance[1]. The significance of a correlation tells us whether the observed relationship is likely to exist in the population or if it could have occurred by chance in our sample.
To test for significance, we typically use a hypothesis test:
- Null Hypothesis (H0): ρ = 0 (no correlation in the population)
- Alternative Hypothesis (Ha): ρ ≠ 0 (correlation exists in the population)
The significance level (α) is the threshold we use to make our decision. Commonly, α = 0.05 is used[3]. If the p-value of our test is less than α, we reject the null hypothesis and conclude that the correlation is statistically significant[4].
For example, if we calculate a Pearson’s r of 0.75 with a p-value of 0.001, we would conclude that there is a statistically significant strong positive correlation between our variables, as 0.001 < 0.05.
Understanding correlation and its significance is essential for media students to interpret research findings, analyze trends, and make data-driven decisions in their future careers.
The Pearson correlation coefficient (r) is a measure of the strength and direction of the linear relationship between two continuous variables. Here’s how to interpret the results:
Strength of Correlation
The absolute value of r indicates the strength of the relationship:
- 0.00 – 0.19: Very weak correlation
- 0.20 – 0.39: Weak correlation
- 0.40 – 0.59: Moderate correlation
- 0.60 – 0.79: Strong correlation
- 0.80 – 1.00: Very strong correlation
Direction of Correlation
The sign of r indicates the direction of the relationship:
- Positive r: As one variable increases, the other tends to increase
- Negative r: As one variable increases, the other tends to decrease
Interpretation Examples
- r = 0.85: Very strong positive correlation
- r = -0.62: Strong negative correlation
- r = 0.15: Very weak positive correlation
- r = 0: No linear correlation
Coefficient of Determination
The square of r (r²) represents the proportion of variance in one variable that can be explained by the other variable[2].
Statistical Significance
To determine if the correlation is statistically significant:
- Set a significance level (α), typically 0.05
- Calculate the p-value
- If p-value < α, the correlation is statistically significant
A statistically significant correlation suggests that the relationship observed in the sample likely exists in the population[4].
Remember that correlation does not imply causation, and Pearson’s r only measures linear relationships. Always visualize your data with a scatterplot to check for non-linear patterns[3].
Citations:
[1] https://statistics.laerd.com/statistical-guides/pearson-correlation-coefficient-statistical-guide.php
[2] https://sites.education.miami.edu/statsu/2020/09/22/how-to-interpret-correlation-coefficient-r/
[3] https://statisticsbyjim.com/basics/correlations/
[4] https://towardsdatascience.com/eveything-you-need-to-know-about-interpreting-correlations-2c485841c0b8?gi=5c69d367a0fc
[5] https://datatab.net/tutorial/pearson-correlation
[6] https://stats.oarc.ucla.edu/spss/output/correlation/
[super_web_share type=”inline” color=”#2271b1″ text=”Share” icon=”share-icon-1″ style=”default” size=”large” align=”start” ] -
Bivariate Analysis: Understanding Correlation, t-test, and Chi Square test
Bivariate analysis is a statistical technique used to examine the relationship between two variables. This type of analysis is often used in fields such as psychology, economics, and sociology to study the relationship between two variables and determine if there is a significant relationship between them.
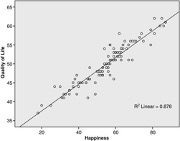
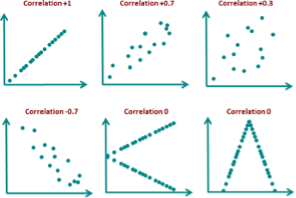
Correlation
Correlation is a measure of the strength and direction of the relationship between two variables. A positive correlation means that as one variable increases, the other variable also increases, and vice versa. A negative correlation means that as one variable increases, the other decreases. The strength of the correlation is indicated by a correlation coefficient, which ranges from -1 to +1. A coefficient of -1 indicates a perfect negative correlation, +1 indicates a perfect positive correlation, and 0 indicates no correlation.
T-Test
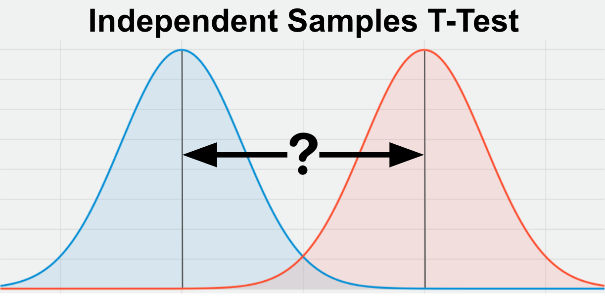
A t-test is a statistical test that compares the means of two groups to determine if there is a significant difference between them. The t-test is commonly used to test the hypothesis that the means of two populations are equal. If the t-statistic is greater than the critical value, then the difference between the means is considered significant.
Chi Square Test
The chi square test is a statistical test used to determine if there is a significant association between two categorical variables. The test measures the difference between the observed frequencies and the expected frequencies in a contingency table. If the calculated chi square statistic is greater than the critical value, then the association between the two variables is considered significant.
Significance
Significance in statistical analysis refers to the likelihood that an observed relationship between two variables is not due to chance. In other words, it measures the probability that the relationship is real and not just a random occurrence. In statistical analysis, a relationship is considered significant if the p-value is less than a set alpha level, usually 0.05.
In conclusion, bivariate analysis is an important tool for understanding the relationship between two variables. Correlation, t-test, and chi square test are three commonly used methods for bivariate analysis, each with its own strengths and weaknesses. It is important to understand the underlying assumptions and limitations of each method and to choose the appropriate test based on the research question and the type of data being analyzed
-
Independent t-test
The independent t-test, also known as the two-sample t-test or unpaired t-test, is a fundamental statistical method used to assess whether the means of two unrelated groups are significantly different from one another. This inferential test is particularly valuable in various fields, including psychology, medicine, and social sciences, as it allows researchers to draw conclusions about population parameters based on sample data when the assumptions of normality and equal variances are met. Its development can be traced back to the early 20th century, primarily attributed to William Sealy Gosset, who introduced the concept of the t-distribution to handle small sample sizes, thereby addressing limitations in traditional hypothesis testing methods. The independent t-test plays a critical role in data analysis by providing a robust framework for hypothesis testing, facilitating data-driven decision-making across disciplines. Its applicability extends to real-world scenarios, such as comparing the effectiveness of different treatments or assessing educational outcomes among diverse student groups.
The test’s significance is underscored by its widespread usage and enduring relevance in both academic and practical applications, making it a staple tool for statisticians and researchers alike. However, the independent t-test is not without its controversies and limitations. Critics point to its reliance on key assumptions—namely, the independence of samples, normality of the underlying populations, and homogeneity of variances—as potential pitfalls that can compromise the validity of results if violated.
Moreover, the test’s sensitivity to outliers and the implications of sample size on generalizability further complicate its application, necessitating careful consideration and potential alternative methods when these assumptions are unmet. Despite these challenges, the independent t-test remains a cornerstone of statistical analysis, instrumental in hypothesis testing and facilitating insights across various research fields. As statistical practices evolve, ongoing discussions around its assumptions and potential alternatives continue to shape its application, reflecting the dynamic nature of data analysis methodologies in contemporary research.